JavaScript数组乱序
本文来自问题及答案如何将一个 JavaScript 数组打乱顺序?
-
首先,毫无疑问: @顾轶灵 轶灵大佬给出的 Fisher–Yates shuffle 洗牌算法 是最完美乱序的算法/方法之一了,正解无疑。
-
同时,很多答案提到了:
[12,4,16,3].sort(function() {
return .5 - Math.random();
});
这样使用 sort 的方法。某些场景下,这样的方法可以使用。但是这不是真正意义上的完全乱序,一些需求中(比如抽奖)这样的写法会出大问题。
- 也有答案提到了优秀的 lodash 库
_.shuffle方法。这也是正解,事实上翻开 lodash 源码相关部分,这个方法正是采用了 Fisher–Yates shuffle 洗牌算法。感兴趣的同学可以进行参阅。
到此,这个回答应该已经有了相对完善的解释。但是最为优秀的码农,还是可以继续“追根问底”。正好现在有点时间,我来针对这几点,稍微解释并拓展一下。
1) 为什么借助 sort 方法不是真正意义上的完全乱序?
先证明不完全性。为此实现一个脚本,我对
var letters = ['A','B','C','D','E','F','G','H','I','J'];
letters 这样一个数组使用 array.sort 方法进行了 10000 次乱序处理,并把乱序的每一次结果可视化输出。每个元素(ABCD...)出现的位置次数进行记录:
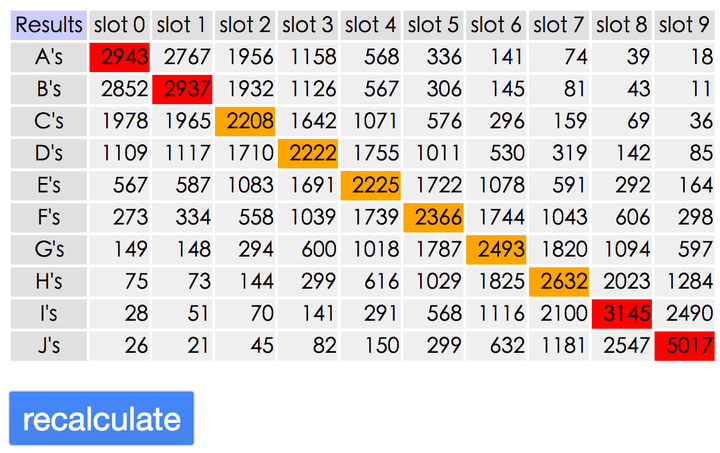
具体脚本实现:HOUCe/shuffle-array
比如 A 元素大概率出现在数组的头部,J 元素大概率出现在数组的尾部,所有元素大概率停留在自己初始位置。
究其原因,在Chrome v8引擎源码中,可以清晰看到。
v8 在处理 sort 方法时,使用了插入排序和快排两种方案。当目标数组长度小于10时,使用插入排序;反之,使用快排。
其实不管用什么排序方法,大多数排序算法的时间复杂度介于 O(n) 到 O(n2) 之间,元素之间的比较次数通常情况下要远小于 n(n-1)/2,也就意味着有一些元素之间根本就没机会相比较(也就没有了随机交换的可能),这些 sort 随机排序的算法自然也不能真正随机。
通俗的说,其实我们使用 array.sort 进行乱序,理想的方案或者说纯乱序的方案是:数组中每两个元素都要进行比较,这个比较有 50% 的交换位置概率。如此一来,总共比较次数一定为 n(n-1)。
而在 sort 排序算法中,大多数情况都不会满足这样的条件。因而当然不是完全随机的结果了。
2) Fisher–Yates shuffle 洗牌算法是什么,为什么满足需求?
这里,我们简单借助图形来理解,非常简单直观。你接下来就会明白为什么这是理论上的完全乱序(图片来源于网络)。
首先我们有一个已经排好序的数组:

Step1:
第一步需要做的就是,从数组末尾开始,选取最后一个元素。

在数组一共 9 个位置中,随机产生一个位置,该位置元素与最后一个元素进行交换。

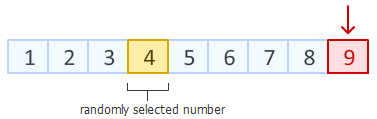
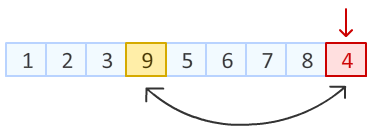
Step2:上一步中,我们已经把数组末尾元素进行随机置换。
接下来,对数组倒数第二个元素动手。在除去已经排好的最后一个元素位置以外的8个位置中,随机产生一个位置,该位置元素与倒数第二个元素进行交换。

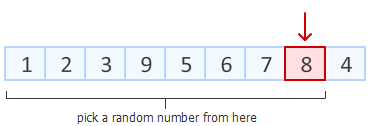

Step3:
理解了前两部,接下来就是依次进行,如此简单。

最后,我们实现代码:
Array.prototype.shuffle = function() {
var array = this;
var m = array.length,
t, i;
while (m) {
i = Math.floor(Math.random() * m--);
t = array[m];
array[m] = array[i];
array[i] = t;
}
return array;
}
当然这种代码不是纯净的,这就属于另一层面的问题了。纯函数与非纯,开发者可以依照自己的开发模式和习惯,自行考虑。
以上,前三段进行了总结。后面大篇幅进行了解释。读者可以根据需要进行阅读。很多内容都是拾人牙慧,探究精神对于程序员来说还是很必要的。
对于 Array.prototype.sort 不够随机问题, 评论区有人给出以下方案:
const random = Math.random;
const shuffle = arr => arr.map(item => {value: item, key: random()})
.sort((a, b) => b.key - a.key)
.map(item => item.value)
